
Prim
Minimum Spanning Tree
최소 신장 트리를 알기 전에 신장 트리 개념에 대해서 알 필요가 있습니다.

신장 트리 (Spanning Tree)
: 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
여기서 사이클이 존재하지 않는 다는 것은 바퀴를 돌아 제자리로 올 수 있다는 것입니다.
신장 트리에는 사이클이 없어야 합니다.
최소 신장 트리는 이러한 신장 트리들 중에서 가중치의 합이 가장 작은 신장 트리를 이릅니다.
MST 라고 하며 이러한 MST 를 구성할 수 있는 알고리즘은 2가지가 있습니다.
바로 Kruskal 알고리즘과 이번 포스팅에서 소개할 Prim 알고리즘 입니다.
2022.10.11 - [✏️ 𝗔𝗹𝗴𝗼𝗿𝗶𝘁𝗵𝗺/개념] - [알고리즘] MST - Kruscal 알고리즘
[알고리즘] MST - Kruscal 알고리즘
Kruscal Minimum Spanning Tree (최소 신장 트리) 최소 신장 트리를 알기 전에 신장 트리 개념에 대해서 알 필요가 있습니다. 신장 트리 (Spanning Tree) : 모든 노드를 포함하면서 사이클이 존재하지 않는 부
yeomss.tistory.com
Prim 특징
1. 시작 정점을 선택한다.
2. 시작 정점에서 갈 수 있는 모든 정점을 우선순위 큐에 담는다.
3. 우선순위 큐에서 정점 하나를 꺼낸다.
4. 만약 해당 정점이 방문하지 않은 정점이라면 MST 에 연결한다.
5. 해당 정점에서 갈 수 있는 방문하지 않은 모든 정점을 우선순위 큐에 담는다.
Prim 알고리즘의 시간 복잡도는 O(ElogV) 입니다.
Prim 예제
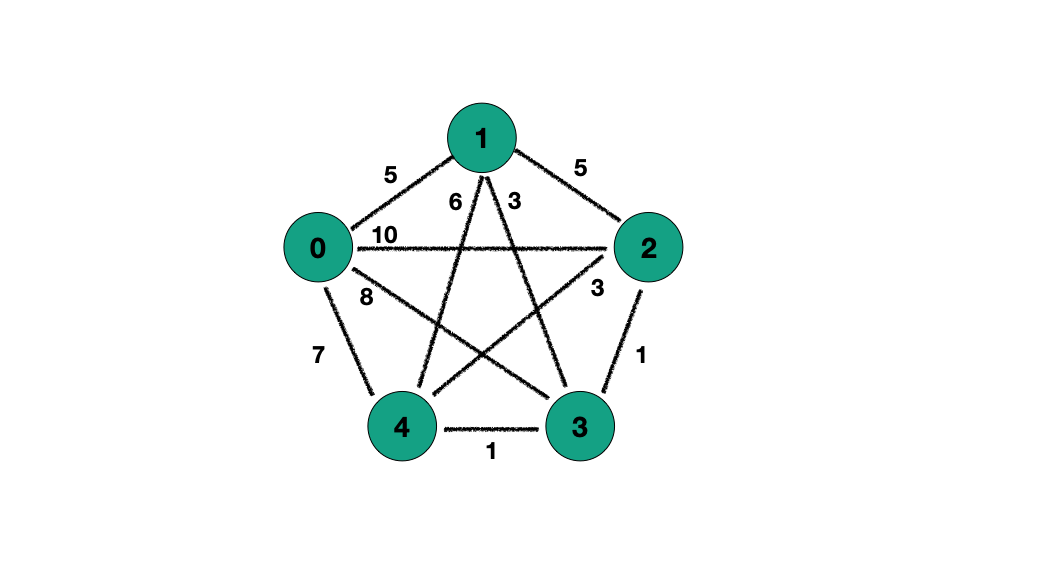
V:5 E:10
from:0 to:1 weight:5
0 2 10
0 3 8
0 4 7
1 2 5
1 3 3
1 4 6
2 3 1
2 4 3
3 4 1다음과 같은 정점들이 있습니다.
노드의 수는 5개 이며 가중치 간선은 10개가 있습니다.
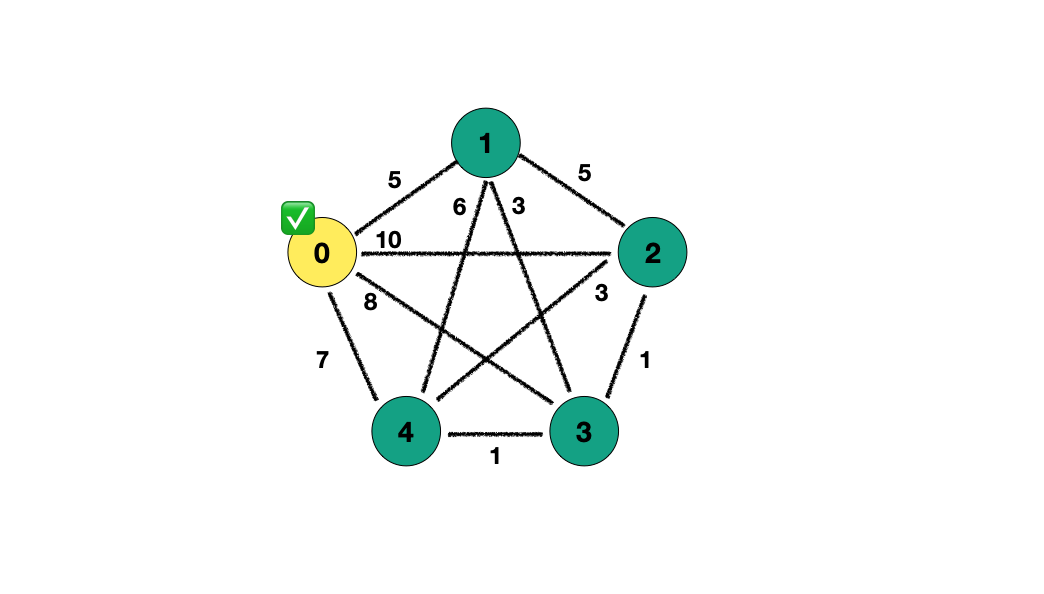
우선 시작 정점을 선택합니다.
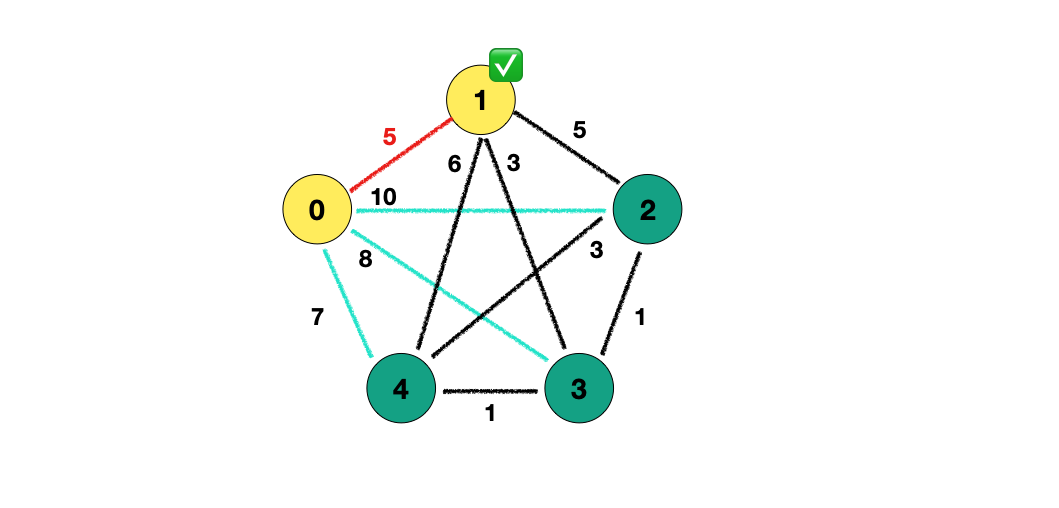
해당 정점에서 갈 수 있는 모든 간선들을 배열에 담습니다.
그러면 { (0, 1), (0, 2), (0, 3), (0, 4) } 가 담깁니다.
여기서 가장 작은 간선을 선택해야 합니다. 우선순위 큐 자료구조를 사용하여 weight 을 기준으로 오름차순 합니다.
그러면 바로 작은 간선을 뽑을 수 있습니다.
가장 가중치가 작은 간선인 (0, 1) 을 선택했습니다.
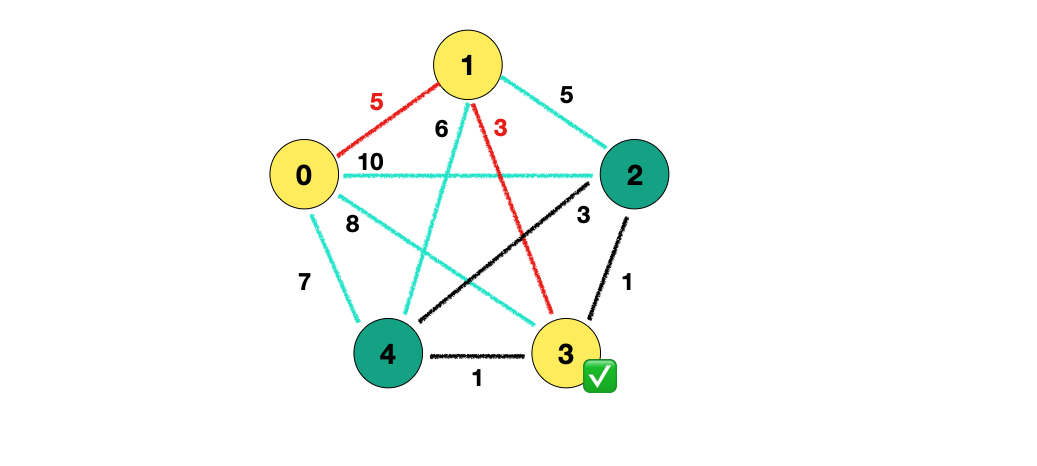
추가한 1 정점에서 갈 수 있는 간선들을 모두 담습니다.
하지만 방문한 정점과의 간선들은 담을 수 없습니다. 이 점을 유의해야 합니다.
따라서 { (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4) } 가 담깁니다. 여기서 제일 작은 가중치를 가진 간선 (1, 3) 을 선택합니다.
이로써 정점 3이 선택되었습니다.
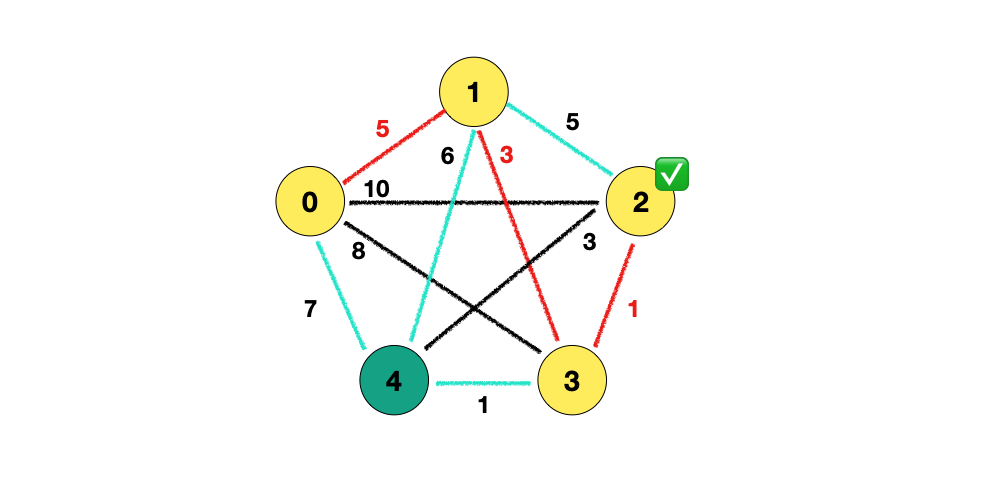
방문한 노드와의 간선은 이제 신경쓰지 않아도 됩니다.
따라서 { (0, 4), (1, 2), (1, 4), (2, 3), (3, 4) } 가 담깁니다. 여기서 가장 작은 간선인 (2, 3) 을 선택하고 정점 2가 선택이 됩니다.
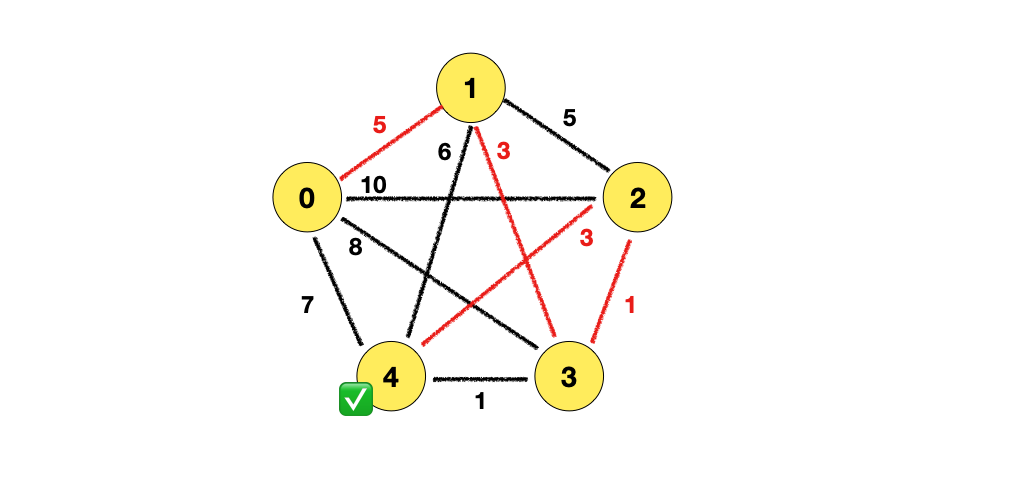
{ (0, 4), (1, 4), (3, 4), (2, 4) } 중에서 가장 작은 가중치의 간선인 (2, 4) 가 선택이 됩니다.
따라서 정점 2가 선택됩니다. 이렇게 최소 스패닝 트리를 만들 수 있습니다.
Prim 알고리즘 input.txt
2
5 10
0 1 5
0 2 10
0 3 8
0 4 7
1 2 5
1 3 3
1 4 6
2 3 1
2 4 3
3 4 1
7 11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
Prim 알고리즘 코드
package first.p05;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class PrimTest {
static int ans, T, V, E;
static ArrayList<ArrayList<Edge>> list = new ArrayList<>(); // 인접 리스트
static boolean[] visit;
// 우선순위 큐
static PriorityQueue<Edge> pq = new PriorityQueue<>((e1, e2) -> (e1.weight - e2.weight));
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("src/first/p05/input/kruskal.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
T = Integer.parseInt(br.readLine());
for (int t = 1; t <= T; t++) {
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
// 초기화
ans = 0;
visit = new boolean[V + 1]; // 0 dummy
list.clear();
pq.clear();
// 인접 리스트 생성
for (int i = 0; i < V; i++) list.add(new ArrayList<>());
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
list.get(from).add(new Edge(to, weight));
list.get(to).add(new Edge(from, weight));
}
// PRIM 알고리즘
prim();
// 출력
System.out.println("#" + t + " " + ans);
}
} // end main
private static void prim() {
// 시작 정점 선택
int idx = 0;
visit[idx] = true;
// 시작 정점에서 갈 수 있는 모든 정점을 pq에 담는다.
pq.addAll(list.get(idx));
while (!pq.isEmpty()) {
Edge edge = pq.poll();
// 이미 방문한 정점이라면 skip
if (visit[edge.to]) continue;
// 새로운 정점 연결
visit[edge.to] = true;
ans += edge.weight; // 가중치 더하기
pq.addAll(list.get(edge.to));
if (++idx == V) break;
}
} // end prim
static class Edge {
int to;
int weight;
public Edge(int to, int weight) {
super();
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge [to=" + to + ", weight=" + weight + "]";
}
} // end Edge
}
인접 리스트를 사용했습니다.
인접 리스트를 사용하기 위해서는 ArrayList<>() 로 각각의 노드를 일단 초기화를 해야합니다.
private static void prim() {
// 시작 정점 선택
int idx = 0;
visit[idx] = true;
// 시작 정점에서 갈 수 있는 모든 정점을 pq에 담는다.
pq.addAll(list.get(idx));
while (!pq.isEmpty()) {
// 우선순위 큐에서 정점 꺼내기
Edge edge = pq.poll();
// 이미 방문한 정점이라면 skip
if (visit[edge.to]) continue;
// 새로운 정점 연결
visit[edge.to] = true;
ans += edge.weight; // 가중치 더하기
pq.addAll(list.get(edge.to));
if (++idx == V) break;
}
} // end prim시작 정점을 선택하고 해당 정점에서 갈 수 있는 모든 정점을 pq에 담습니다.
그런 다음 pq 에서 정점을 꺼냅니다.
만약 방문한 정점이라면 넘어갑니다. 방문하지 않은 정점이라면 visit 처리를 해줍니다.
그리고 나서 해당 정점에서 갈 수 있는 모든 간선들을 pq에 추가해줍니다.
# Prim java # MST Prim # Prim 알고리즘
'✏️ 𝗔𝗹𝗴𝗼𝗿𝗶𝘁𝗵𝗺 > 개념' 카테고리의 다른 글
| [알고리즘] 최단경로 - Dijkstra 알고리즘 (0) | 2022.10.11 |
|---|---|
| [알고리즘] MST - Kruscal 알고리즘 (0) | 2022.10.11 |
| [알고리즘] Next Permutation (0) | 2022.09.13 |
| [알고리즘] Bit Masking (2) | 2022.09.12 |
| [알고리즘] 슬라이딩 윈도우 개념 및 문제 (0) | 2022.08.08 |
![[알고리즘] MST - Prim 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F99fSP%2FbtrOhXhFIHP%2F0NWNtxZCIR4SSLD7ESHznK%2Fimg.png)