
✅ 탐색이란? (Search)
알고리즘에서 탐색 개요
◾ 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정
◾ 프로그래밍에서는 그래프, 트리 등의 자료구조 안에서 탐색하는 문제가 자주 등장한다.
◾ 대표적인 탐색 알고리즘
- DFS
- BFS
◾ 자료구조란?
- 데이터를 표현하고 관리 및 처리하기 위한 구조
◾ DFS/BFS에서 사용하는 자료구조
- 스택 ➡ LIFO (Last In First Out)
- 큐 ➡ FIFO (First In First Out)
◾ 그래프란?
- 노드 (Node, Vertex) 와 간선 (Edge)로 이루어진 자료구조
- 인접 행렬, 인접 리스트로 표현된다.
✅ DFS (Depth-First Search)
깊이 우선 탐색
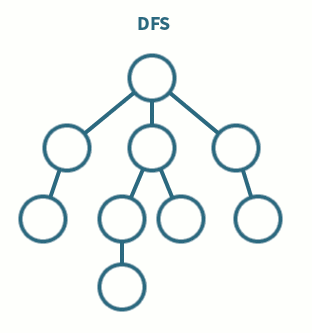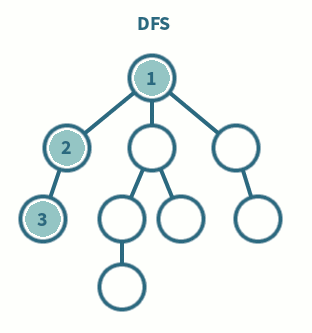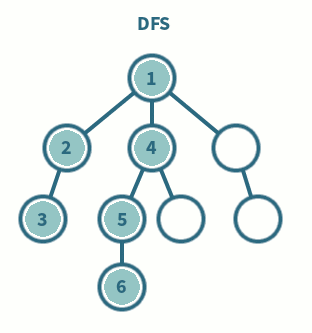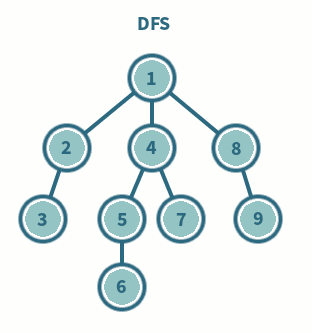
◾ 깊이 우선 탐색이라고 부른다.
◾ 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
◾ 스택 및 재귀함수를 이용하여 구현한다.
📚 DFS 알고리즘
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2-1. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 해당 인접 노드를 스택에 넣고, 방문처리를 한다.
2-2. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
📚 시간 복잡도
◾ 노드의 수 V, 간선의 수 E 라고 가정.
| 구현 방법 | 시간복잡도 |
| 인접 리스트 | O(V + E) |
| 인접 행렬 | O(V^2) |
📚 구현 코드

◾ 인접 리스트 사용
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [0] * 9
def DFS(graph, v, visited):
visited[v] = 1
print(v, end = ' ')
for i in graph[v]:
if visited[i] == 0:
DFS(graph, i, visited)
DFS(graph, 1, visited)◾ 인접 행렬 사용
INF = 999999
graph = [
[INF, INF, INF, INF, INF, INF, INF, INF, INF], # 0
[INF, INF, 1, 1, INF, INF, INF, INF, 1], # 1
[INF, 1, INF, INF, INF, INF, INF, 1, INF], # 2
[INF, 1, INF, INF, 1, 1, INF, INF, INF], # 3
[INF, INF, INF, 1, INF, 1, INF, INF, INF], # 4
[INF, INF, INF, 1, 1, INF, INF, INF, INF], # 5
[INF, INF, INF, INF, INF, INF, INF, 1, INF], # 6
[INF, INF, 1, INF, INF, INF, 1, INF, 1], # 7
[INF, 1, INF, INF, INF, INF, INF, 1, INF] # 8
]
visited = [0] * len(graph[0])
def DFS(graph, v, visited):
visited[v] = 1
print(v, end=' ')
for i in range(1, len(graph[0])):
if visited[i] == 0:
if graph[v][i] == 1:
DFS(graph, i, visited)
DFS(graph, 1, visited)
✅ BFS (Breadth-First Search)
너비 우선 탐색

◾ 너비 우선 탐색이라고 부른다.
◾ 가까운 노드부터 탐색하는 알고리즘
◾ 큐를 이용하여 구현한다.
◾ DFS보다 빠르다.
📚 BFS 알고리즘
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
📚 시간 복잡도
◾ 노드의 수 V, 간선의 수 E 라고 가정.
| 구현 방법 | 시간복잡도 |
| 인접 리스트 | O(V + E) |
| 인접 행렬 | O(V^2) |
📚 구현 코드

◾ 인접 리스트 사용
from collections import deque
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [0] * 9
def BFS(graph, start, visited):
queue = deque([start])
visited[start] = 1
while queue:
v = queue.popleft()
print(v, end = ' ')
for i in graph[v]:
if visited[i] != 1:
queue.append(i)
visited[i] = 1
BFS(graph, 1, visited)◾ 인접 행렬 사용
from collections import deque
INF = 999999
graph = [
[INF, INF, INF, INF, INF, INF, INF, INF, INF], # 0
[INF, INF, 1, 1, INF, INF, INF, INF, 1], # 1
[INF, 1, INF, INF, INF, INF, INF, 1, INF], # 2
[INF, 1, INF, INF, 1, 1, INF, INF, INF], # 3
[INF, INF, INF, 1, INF, 1, INF, INF, INF], # 4
[INF, INF, INF, 1, 1, INF, INF, INF, INF], # 5
[INF, INF, INF, INF, INF, INF, INF, 1, INF], # 6
[INF, INF, 1, INF, INF, INF, 1, INF, 1], # 7
[INF, 1, INF, INF, INF, INF, INF, 1, INF] # 8
]
visited = [0] * len(graph[0])
def BFS(graph, start, visited):
queue = deque([start])
visited[start] = 1
while queue:
v = queue.popleft()
print(v, end = ' ')
for i in range(1, len(graph[0])):
if visited[i] == 0:
if graph[v][i] == 1:
queue.append(i)
visited[i] = 1
BFS(graph, 1, visited)
# 이것이코딩테스트다 DFS/BFS
# DFS/BFS 개념
# DFS BFS 인접리스트
# DFS BFS 인접행렬
728x90
'✏️ 𝗔𝗹𝗴𝗼𝗿𝗶𝘁𝗵𝗺 > 개념' 카테고리의 다른 글
| [알고리즘] 슬라이딩 윈도우 개념 및 문제 (0) | 2022.08.08 |
|---|---|
| [알고리즘] Queue 개념 + java.util.Queue (0) | 2022.08.06 |
| [알고리즘] Stack 개념 + java.util.Stack (0) | 2022.08.06 |
| [알고리즘] 순열, 조합, 부분집합 + 구현 (0) | 2022.08.06 |
| [알고리즘] 개요, 시간복잡도 효율성 etc (0) | 2021.11.23 |
![[알고리즘] DFS, BFS + 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fec0icb%2FbtrI3tMmIaD%2Fcl2CrrgPtFFTbcpo9aJGyK%2Fimg.png)