
순열 (Permutation)
개념
순열이란?
: 순서를 고려하여 서로 다른 것들 중 몇 개를 뽑아 한 줄로 나열하는 것

자리의 순서를 고려합니다.
즉, 조합과는 다르게 1-2-3 과 2-3-1 을 다르게 봅니다.
구현
package day220804.practice;
import java.util.Arrays;
import java.util.Scanner;
public class Permutation {
static int N, K;
static int[] numbers;
static boolean[] isSelected;
private static void perm(int cnt) {
// 기저 조건
if (cnt == K) {
System.out.println(Arrays.toString(numbers));
return;
}
// 숫자를 뽑는 것이 반복적인 일이다.
for (int i = 1; i <= N; i++) {
if (isSelected[i]) continue;
// 내가 해야하는 일
numbers[cnt] = i;
isSelected[i] = true;
// 다음 재귀 호출
perm(cnt + 1);
isSelected[i] = false;
}
}
// 순열 -> 순서를 중요하게 생각한다.
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
numbers = new int[K];
isSelected = new boolean[N + 1];
perm(0);
}
}
일단 모든 경우의 수를 돌아야 하기에 for 문을 넣습니다.
그리고 isSelected 배열을 둬서 해당 숫자를 선택했는지 안했는지 확인을 합니다.
만약 선택을 했다면 넘어갑니다.
중복 순열 (Permutation with Repetition)
개념
중복을 허용하여 순열을 하는 것을 이릅니다.
즉, 원래는 1-2-3 이렇게 뽑아야 했지만 이제는 1-1-1 이렇게도 가능한 것입니다.
뽑을 수 있는 선택지가 이전 것 까지 늘어납니다.
구현
package day220804.practice;
import java.util.Arrays;
import java.util.Scanner;
public class DuplicatedPermutation {
static int N, K;
static int[] numbers;
// 중복 순열
private static void duperm(int cnt) {
if (cnt == K) {
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = 1; i <= N; i++) {
numbers[cnt] = i;
duperm(cnt + 1);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
numbers = new int[K];
duperm(0);
}
}
isSelected 배열을 없애주면 중복순열이 됩니다.
조합 (Combination)
개념
조합이란?
: 순서를 고려하지 않고 서로 다른 것들 중에서 몇 개를 뽑는 것

조합은 순서를 고려하지 않습니다.
즉슨, 1-2-3 이나 2-3-1 이나 똑같이 보는 것입니다.
순서를 고려하고, 고려하지 않고 가 바로 순열과 조합을 구별하는 특징입니다.
예를 들어, 복권을 뽑는 것은 결론적으로 순서와 상관없이 번호만 맞으면 되므로 조합에 해당합니다.
구현
package day220804.practice;
import java.util.Arrays;
import java.util.Scanner;
public class Combination {
static int N;
static int K;
static int[] numbers;
private static void comb(int cnt, int start) {
// 기저 조건
if (cnt == K) {
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = start + 1; i <= N; i++) {
// 내가 해야하는 일
numbers[cnt] = i;
// 다음 재귀 호출
comb(cnt + 1, i);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
numbers = new int[K];
comb(0, 0);
}
}
조합은 이전의 것들은 굳이 보지 않아도 됩니다.
따라서 start 매개변수를 이용하여 다음 것들 부터 시작합니다.
중복 조합 (Combination)
개념
뽑는 것에 있어 중복을 허용하여 조합을 뽑습니다.
즉, 1-1-2 도 된다는 것입니다.
구현
package day220804.practice;
import java.util.Arrays;
import java.util.Scanner;
public class DuplicatedCombination {
static int N, K;
static int[] numbers;
// 중복 조합
private static void ducomb(int cnt, int start) {
if (cnt == K) {
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = start; i <= N; i++) {
numbers[cnt] = i;
ducomb(cnt + 1, i);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
K = sc.nextInt();
numbers = new int[K];
ducomb(0, 1);
}
}다음 것을 보던 걸 현재로 바꾸면 중복을 허용하게 됩니다.
부분 집합 (Subset)
개념
부분집합이란?
: 해당 집합의 원소들로만 이루어진 집합.
즉, B가 A의 부분집합이라면 B의 모든 원소가 A에 속하게 된다.

부분 집합은 2^k 와 같습니다.
해당 원소가 만들고자하는 부분집합에 속하고, 속하지 않고를 따지기 때문입니다.
구현
package day220804.practice;
import java.util.Scanner;
public class SubSet {
static int N;
static boolean[] isSelected;
private static void subset(int idx) {
// 기저 조건
if (idx == N) {
for (int i = 0; i < N; i++) {
System.out.print(isSelected[i] ? (i + 1) : "X");
System.out.print("\t");
}
System.out.println();
return;
}
// 선택 했다.
isSelected[idx] = true;
subset(idx + 1);
// 선택하지 않았다.
isSelected[idx] = false;
subset(idx + 1);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
isSelected = new boolean[N];
subset(0);
}
}
선택을 하고 재귀함수를 호출하여 계속 탐색을 해냅니다.
그리고 빠져나와 선택하지 않은 경우의 수를 따집니다.
여기서 isSelected 배열의 i 은 1 - N 까지의 수의 인덱스에 해당합니다.
부분집합의 합 문제
주어지는 부분집합의 합이 0 일때, 해당 부분집합을 출력하라.
[입력]
5
-7 -3 -2 5 8
[출력]
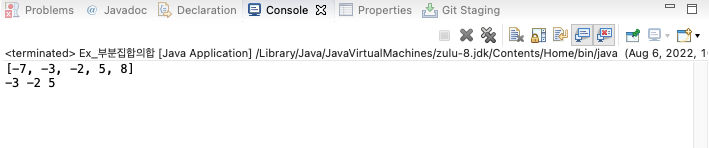
-3 -2 5
package day220804.problem;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
//5
//-7 -3 -2 5 8
public class Ex_부분집합의합 {
static int N;
static int[] arr;
static boolean[] isSelected;
// 부분집합의 합이 0이 되는지 확인하는 문제
private static void subset(int idx) {
if (idx == N) {
int sum = 0;
for (int i = 0; i < N; i++) {
if (isSelected[i]) sum += arr[i];
}
if (sum == 0) {
for (int i = 0; i < N; i++) {
System.out.print(isSelected[i] ? arr[i] + " " : "");
}
System.out.println();
}
// for (int i = 0; i < N; i++) {
// System.out.print(isSelected[i] ? arr[i] : " ");
// System.out.print("\t");
// }
//
// System.out.println();
return;
}
isSelected[idx] = true;
subset(idx + 1);
isSelected[idx] = false;
subset(idx + 1);
}
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("input.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
arr = new int[N];
isSelected = new boolean[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
System.out.println(Arrays.toString(arr));
subset(0);
}
}
# java 순열 구현 # java 조합 구현 # java 부분집합 구현 # java 재귀 # 알고리즘 순열 조합 부분집합
# 알고리즘 순열 # 알고리즘 조합 # 알고리즘 부분집합
'✏️ 𝗔𝗹𝗴𝗼𝗿𝗶𝘁𝗵𝗺 > 개념' 카테고리의 다른 글
| [알고리즘] 슬라이딩 윈도우 개념 및 문제 (0) | 2022.08.08 |
|---|---|
| [알고리즘] Queue 개념 + java.util.Queue (0) | 2022.08.06 |
| [알고리즘] Stack 개념 + java.util.Stack (0) | 2022.08.06 |
| [알고리즘] DFS, BFS + 구현 (0) | 2021.11.28 |
| [알고리즘] 개요, 시간복잡도 효율성 etc (0) | 2021.11.23 |
![[알고리즘] 순열, 조합, 부분집합 + 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FuweBU%2FbtrI6qO9VBa%2FkkBi2566tma6wwSx6tZlC0%2Fimg.png)