
🚩 문제 설명
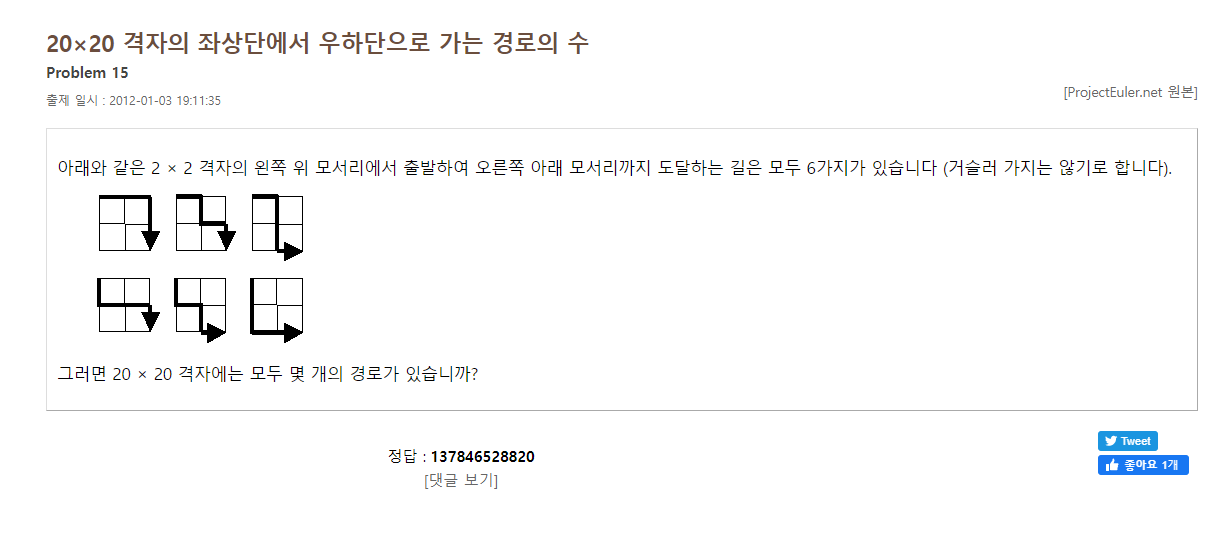
◾ 20 x 20 격자의 좌상단에서 우하단으로 가는 경로의 수를 구하는 문제
◾ 다이나믹 프로그래밍 문제로 보인다.
📑 문제 풀이
#include <iostream>
#include <ctime>
#define ll long long
using namespace std;
ll d[21][21];
ll grid(ll r, ll c)
{
if (d[r][c] > 0) return d[r][c];
if (r == 0 && c == 0) return 1;
if (r == 1)
{
d[r][c] = c + 1;
}
else if (c == 1)
{
d[r][c] = r + 1;
}
else
{
d[r][c] = grid(r, c - 1) + grid(r - 1, c);
}
return d[r][c];
}
int main()
{
clock_t start, end;
start = clock();
cout << grid(20, 20) <<'\n';
end = clock();
cout << '\n\n'<< (double)(end-start) << "(ms)" << '\n';
return 0;
}💬 Point
👉 다이나믹 프로그래밍 문제
👉 D[r][c] = D[r][c-1] + D[r-1][c]
◾ DP로 문제를 풀 수 있다.
◾ 나는 DP 방식중에서 재귀를 사용하였다.
◾ memoizaion을 활용해 d[][] 라는 이차원 배열을 만들어준다.
- 만약 memoization 되어있는 배열의 수를 꺼낸다면
- 바로 return을 해서 시간을 단축시킨다.
◾ 좌상단에서 우하단으로 가는 방법은 수평 블록과 수직 블록이 합쳐져서 만들어지는 것이다.
◾ 예를 들어 D[1][1]은 다음과 같이 2가지 방법이 있다.
- r + c
- c + r

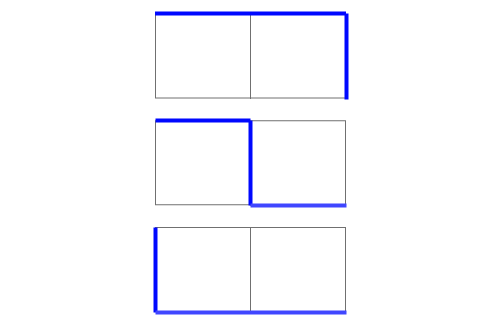
◾ D[1][2]은 다음과 같다. 이러한 수평 블록은 r이 늘어나는 만큼 갯수가 증가한다.
- r + r + c
- r + c + r
- c + r + r
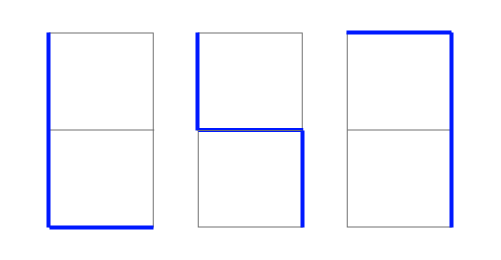
◾ D[2][1]은 다음과 같다. 이러한 수직 블록은 c가 늘어나는 만큼 갯수가 증가한다.
- c + c + r
- c + r + c
- r + c + c
◾ 만약 D[3][3] 사각형이라면 D[2][1]과 D[1][2] 사각형의 경로의 갯수를 합친것과 같다.
◾ 따라서 D[r][c] = D[r][c-1] + D[r-1][c] 의 점화식을 따른다.
But,
✅ 경로의 수 같은 문제는 조합을 구현하면 쉽게 풀 수 있다.
➕ 풀이 사이트 첨부
https://www.mathblog.dk/project-euler-15/
Project Euler 15: Routes through a 20x20 grid n C# | MathBlog
Given problem 15 of Project Euler which reads How many routes are there through a 20x20 grid? I propose two different solution approaches. One which is heavily inspired by dynamic programming and one which uses combinatorics. Both solutions are efficient a
www.mathblog.dk
➕ 풀이 사이트 첨부
https://opentutorials.org/course/3186/17530
프로젝트 오일러 15번문제 - 경로의 갯수 - 파이썬 실전 프로젝트
격자의 끝에서 끝으로 이동하는 경로의 갯수를 구하는 문제입니다. (모바일에서, 그림이 안보이시면 새로고침 한번 해주시면 됩니다.) Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there
opentutorials.org
'✏️ 𝗔𝗹𝗴𝗼𝗿𝗶𝘁𝗵𝗺 > etc' 카테고리의 다른 글
| Problem #019 (0) | 2020.02.17 |
|---|---|
| Problem #017 (0) | 2020.02.11 |
| Problem #014 (0) | 2020.02.05 |
| Problem #013 (0) | 2020.02.04 |
| Problem #011 (0) | 2020.01.31 |
