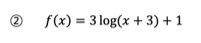해당 내용은 다음 출처에서 가져왔습니다.
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
SSAFY 시리즈
1. [후기] SSAFY 8기 지원과정 (자소서/코딩테스트)
2. [후기] SSAFY 8기 지원과정 (면접)
수와 표현
컴퓨터상에서의 수의 표현
- 컴퓨터는 0과 1을 표현할 수 있는 비트들을 모아 수로 표현한다.
- 전구를 생각해보라.
- on / off
- k 개의 비트를 사용하면 0부터 2^k - 1 까지 표현이 가능하다.
- 컴퓨터 과학에서 로그는 이진로그를 사용한다. (밑 2 생략하고 표현)
n 을 표현하기 위해서 필요한 bit의 개수
- 어떤 값 n 을 표현하기 위해서 몇 개의 비트가 필요할까?
- 이는 2^k - 1 >= n 이 성립해야함을 이른다.
- 즉, 2^k >= (n + 1) 와도 같다.
- 여기에 로그를 취하게 되면
- k >= log(n+1) 이 된다.
- 즉, k 를 나타내기 위해선 log(n+1) 개의 비트가 필요하다.
x = log(n)
- 2의 몇 승이 n이 되는가?
- n 을 표현하는 데 몇 비트가 필요한가?
- 1로 시작해서 계속 2배를 할 때, 몇 번 하면 n이 되는가?
- n을 2로 계속 나눌 때 몇 번을 나누면 거의 1이 되는가?
- 위 공식은 위와 같은 질문들의 답이 될 수 있다.
- x와 n을 비교할 때, n이 기하급수적으로 커지면 x와 n의 차이가 엄청나게 커진다.
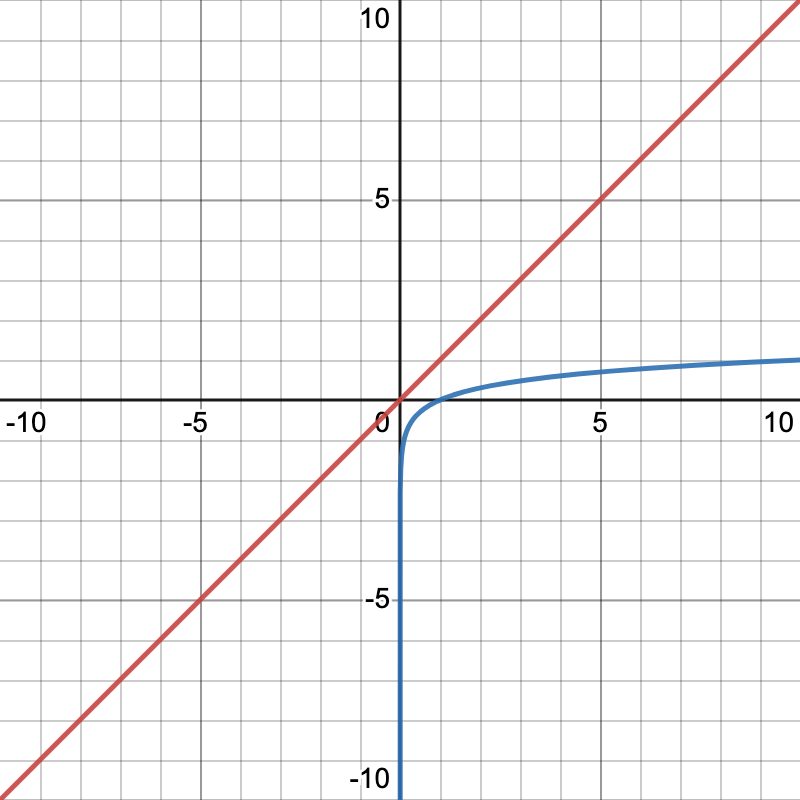
- 이는 그래프만 그려봐도 알 수 있다.
32비트의 컴퓨터에는 몇 개의 주소공간이 있는가?

- 2^32 ~= 40 억개의 주소 공간을 다루고 있다.
nlog(n) Why?
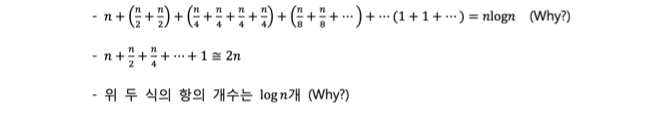
- 왜 해당 공식이 nlogn 이 되는걸까?
- 증명을 하자면 다음과 같다. (트리 높이 공식을 이용하면 된다.)

- 이렇게 완전 이진 트리의 모양으로 나타낼 수 있고, 해당 트리의 모든 노드의 갯수를 한번 구해보자.

- 트리의 총 노드의 갯수는 등비급수 합 공식으로 구할 수 있다.
- 여기서 모든 노드의 갯수를 n개라고 가정하고, 트리의 높이 h를 구해보자.
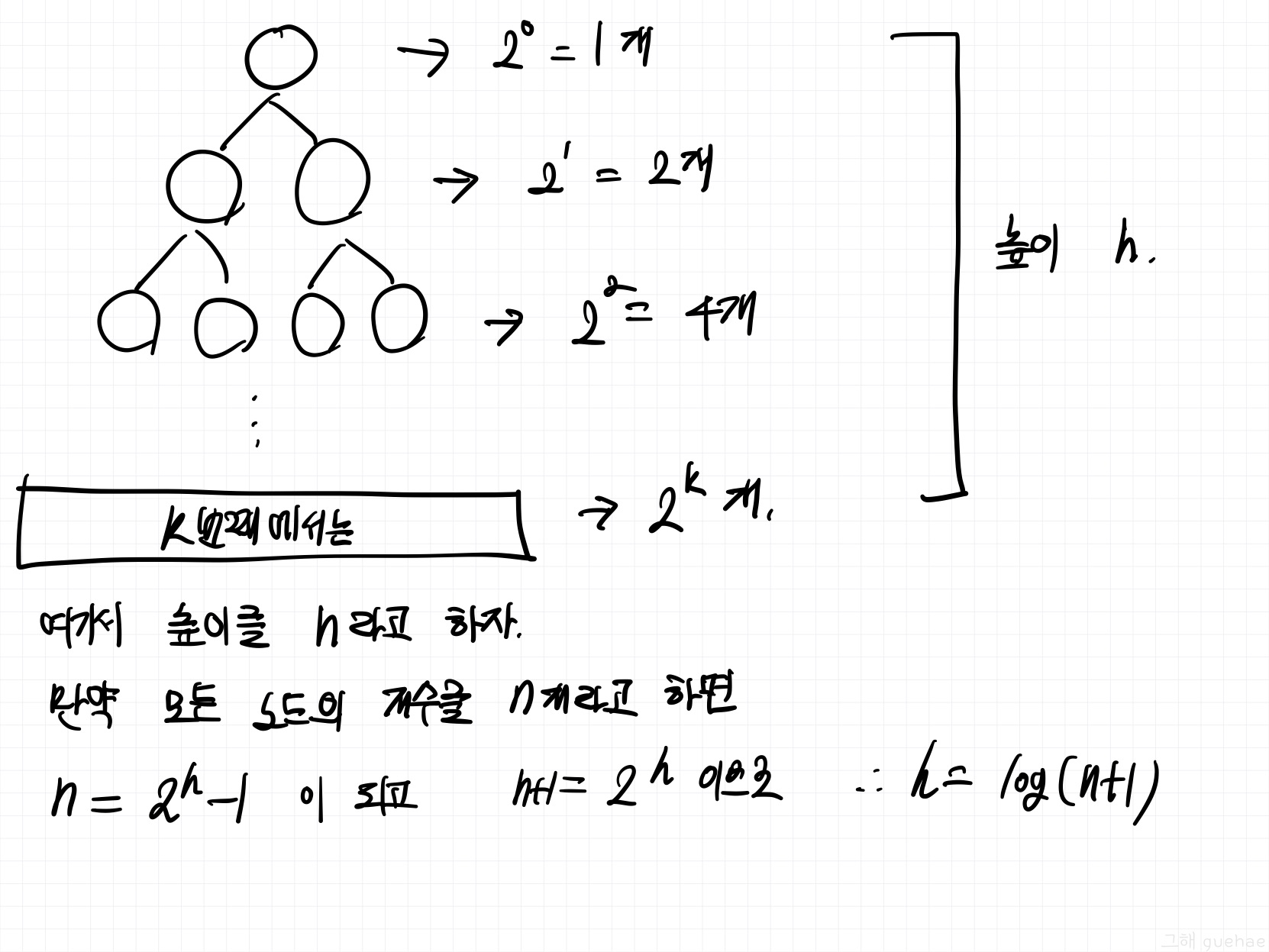
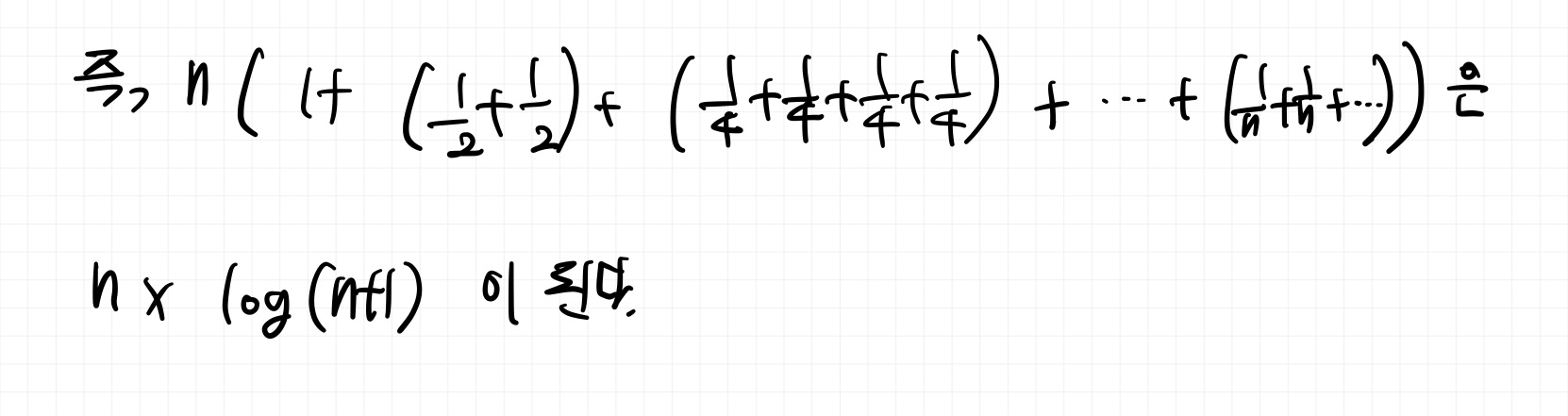
- 따라서 nlog(n+1) 이 되는 것이다.
- n + n/2 + n/4 + .. + 1 이 2n이 되는 과정은 아래와 같다.

연습 문제
Q. 2진수 표현에서 log(n) 비트로 표현할 수 있는 숫자 범위는?
k bit 를 가질 때, 0부터 2^k - 1 의 수까지 나타낼 수 있다.
따라서, log(n) bit 를 가진다면 0 부터 2^(log(n)) - 1 의 수까지 나타낼 수 있다.
Q. 스무고개가 이상적으로 진행된다고 할 때, 맞출 수 있는 답의 종류는 몇가지 인가?
스무고개는 정답이 맞고, 틀리고의 문제이다.
따라서 이진법으로 나타낼 수 있다.
총 20개의 문제가 나오니 맞았을 때, 틀렸을 때 경우를 따져
2 x 2 x ... x 2 해서
2^20 개의 답의 종류가 나올 수 있다.
Q. n이 충분히 큰 값일 때 다음 중 어느 값이 더 큰가?
각 쌍에 대해 비교하고 그 이유를 작성하시오.

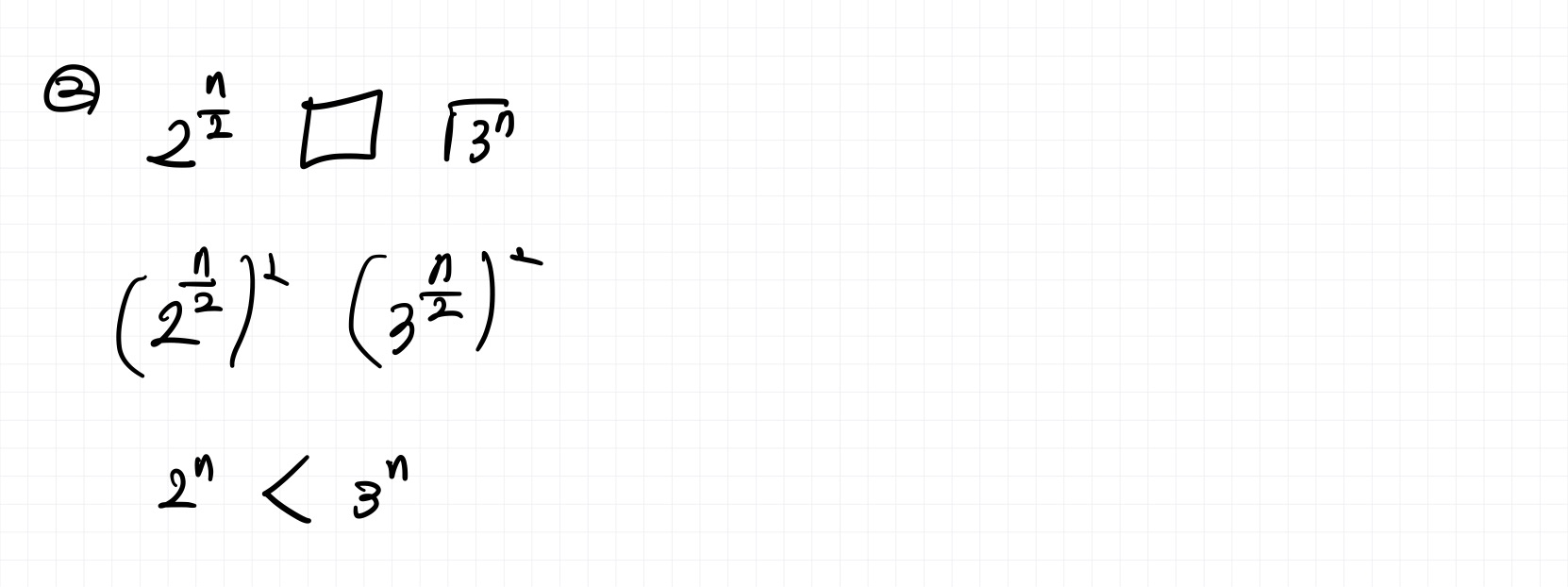

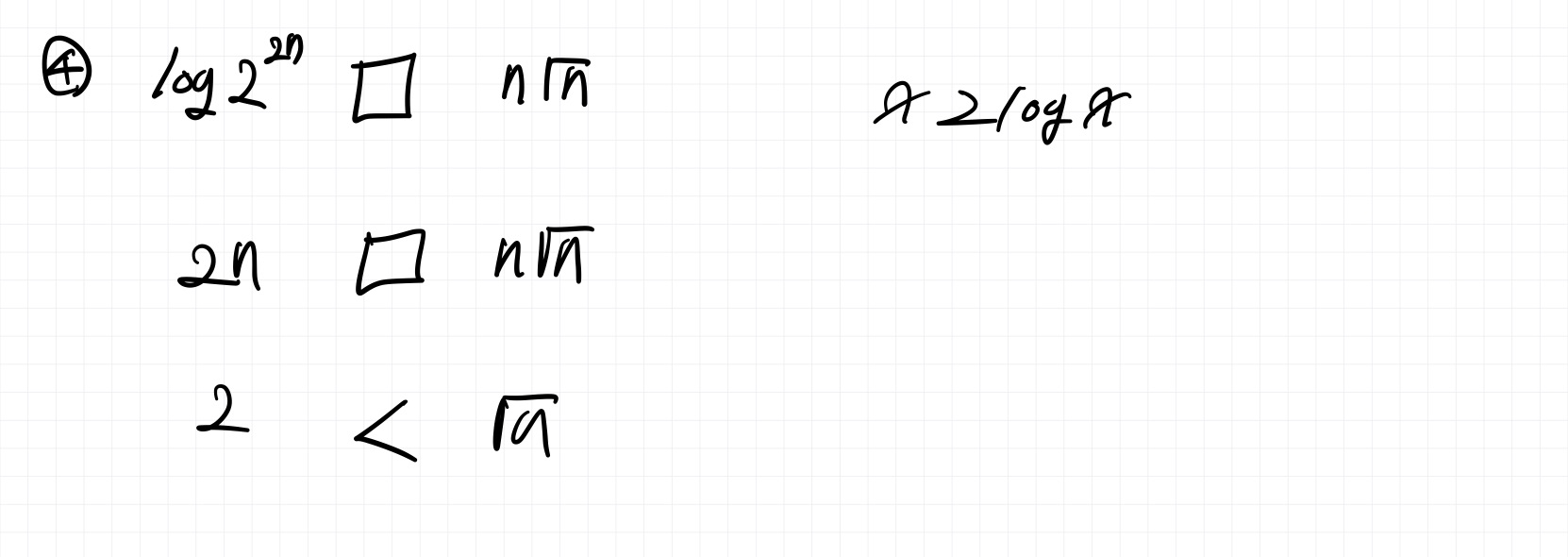
Q. x = log_a(yz) 일 때 x를 2를 밑으로 하는 로그들로 표현하시오.
(단, 로그 함수의 인자는 모두 문자 하나여야 한다.)

Q. 다음 함수들의 역함수를 구하시오.

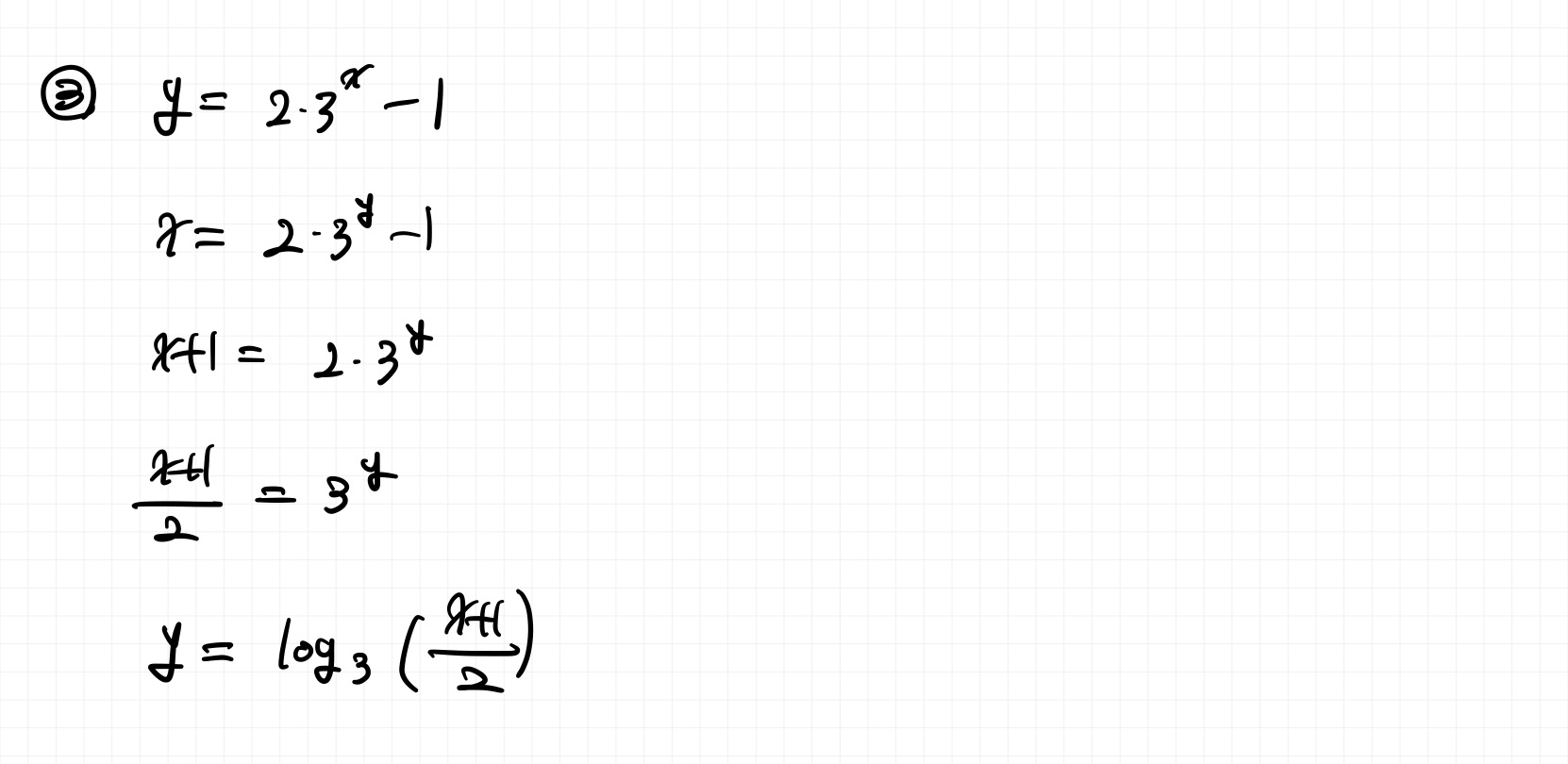
회고
흠 맞게 풀었나 잘 모르겠다.
그래도 그냥 푼 거에 의의를 두자^__^
# swea 논리와 증명 # swae nlogn # SWEA nlogn # SWEA 풀이 # SWEA 수와 표현 # 수와 표현 풀이 # swea 수와표현 nlogn
728x90
'⛺ 𝗕𝗼𝗼𝘁 𝗖𝗮𝗺𝗽 > SSAFY 8기' 카테고리의 다른 글
| [TIL] 변수, 형변환, 배열, 객체, 메서드 (1) | 2022.07.18 |
|---|---|
| [TIL] Day 4 - Computational Thinking (0) | 2022.07.11 |
| [TIL] Day 2 - Computational Thinking (0) | 2022.07.05 |
| [TIL] Day 1 - Computational Thinking (2) | 2022.07.04 |
| [후기] SSAFY 8기 지원과정 (면접) (3) | 2022.07.01 |
![[TIL] Day 3 - Computational Thinking](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbUj4rQ%2FbtrGBjxNErk%2FFqmDrJNxUsI4d69TFJwX9K%2Fimg.png)