[TIL] Day 2 - Computational Thinking

해당 내용은 다음 출처에서 가져왔습니다.

https://swexpertacademy.com/main/learn/course/subjectList.do?courseId=AVuPCwCKAAPw5UW6&subjectId=AV1lGr4qAAYCFAb_ 

SW Expert Academy

SSAFY 시리즈
1. [후기] SSAFY 8기 지원과정 (자소서/코딩테스트)
2. [후기] SSAFY 8기 지원과정 (면접)
3. [TIL] Day 1 - Computational Thinking
4. [TIL] Day 2 - Computational Thinking
5. [TIL] Day 3 - Computational Thinking

---

 

 

 논리와 증명 

연습 문제

Q. 다음 명제들이 항진명제라는 것을 진리표를 이용해서 보이시오.
1) ~(~p ∧ q) ∨ q
2) (~p ∨ q) ∨ (p ∧ ~q)

• 항진명제 라는 것은 어떤 해석에서도 항상 참이 되는 명제를 이른다.
• 그니까 경우의 수를 따져봤을 때 다 T 이면 항진명제인 것이다.

1)

p	q	~(~p ∧ q)	~(~p ∧ q) ∨ q
T	T	not (F and T = F) = T	T
T	F	not (F and F = F) = T	T
F	T	not (T and T = T) = F	T
F	F	not (T and F = F) = T	T

∴ 항진명제이다.

2)

p	q	(~p ∨ q)	(p ∧ ~q)	(~p ∨ q) ∨ (p ∧ ~q)
T	T	F or T = T	T and F = F	T
T	F	F or F = F	T and T = T	T
F	T	T or T = T	F and F = F	T
F	F	T or F = T	F and T = F	T

∴ 항진명제이다.

 

Q. 다음 명제들이 모순명제라는 것을 진리표를 이용해서 보이시오.
1) (~p ∨ q) ∧ (p ∧ ~q)
2) (p ∧ q) ∧ (p ∧ ~q)

• 모순명제라는 것은 어떤 해석에서도 항상 거짓이 되는 명제를 이른다.
• 항진명제의 항등원
• 경우를 따졌을 때, 모두 F 이면 모순명제인 것이다.

1)

p	q	(~p ∨ q)	(p ∧ ~q)	(~p ∨ q) ∧ (p ∧ ~q)
T	T	F or T = T	T and F = F	F
T	F	F or F = F	T and T = T	F
F	T	T or T = T	F and F = F	F
F	F	T or F = T	F and T = F	F

∴ 모순명제이다.

2)

p	q	(p ∧ q)	(p ∧ ~q)	(p ∧ q) ∧ (p ∧ ~q)
T	T	T and T = T	T and F = F	F
T	F	T and F = F	T and T = T	F
F	T	F and T = F	F and F = F	F
F	F	F and F = F	F and T = F	F

∴ 모순명제이다.

 

Q. 다음 명제의 쌍 들에 대해서 두 명제가 동등한지를 진리표를 이용해 확인하시오.
1) p ∧ (p ∨ q) 와 p
2) ~p ∨ ~ q 와 ~(p ∨ q)

1)

p	q	p ∧ (p ∨ q)	equal
T	T	T and (T or T = T) = T	O
T	F	T and (T or F = T) = T	O
F	T	F and (F or T = T) = F	O
F	F	F and (F or F = F) = F	O

∴ 동등하다.

2)

p	q	~p ∨ ~ q	~(p ∨ q)	equal
T	T	F or F = F	not (T or T = T) = F	O
T	F	F or T = T	not (T or F = T) = F	X
F	T	T or F = T	not (F or T = T) = F	X
F	F	T or T = T	not (F or F = F) = T	O

∴ 동등하지 않다.

 

Q. 명제식의 변형을 통하여 다음 명제를 간소화하시오.
1) (p ∧ ~q) ∨ (p ∧ q)
2) (p ∨ ~q) ∧ (~p ∨ ~q)

02_1.pdf

0.14MB

• 참고하시면 좋을 파일입니다.
• http://contents.kocw.or.kr/document/lec/2011/chungbuk/teaching/02_1.pdf

1)
p and (~q or q)
-> p and T
-> p

2)
(p and ~p) or ~ q
-> F or ~q
-> ~q

 

Q. 다음 명제들이 참인지 확인하시오.
단, R은 실수의 집합을 의미하고, Z는 정수의 집합을 의미한다.

• 전칭기호 ∀
• 존재기호 ∃
• ∀x(B(x) → C(x)) 모든 x에 대하여 x가 자연수이면 x는 정수이다.
• ∃x(B(x) ∧ C(x)) 어떤 x에 대하여 자연수이면서 정수인 x가 적어도 하나 존재한다.

1)
실수인 모든 x에 대하여, x^2 >= x 이다.
1/2을 넣어보면 알 수 있다.  거짓이다.
혹은 x(x-1) >= 0 이 되는데 이는 그래프를 그려보면 0 < x < 1 에서 음수가 된다.
∴ 거짓

2)
정수인 모든 x에 대하여, x^2 >= x 이다.
정수는 +- 기호가 붙은 모든 자연수를 이른다. 분수는 들어가지 않는다.
따라서, 모든 x 의 절대값은 양수가 되고 이는 0 < x < 1 이라는 범위에 들어가지 않는다.
∴ 참

3)
실수인 어떤 x에 대하여, x^2 < x 이다.
이항을 하면 x(x-1) < 0 이 되고 그래프를 그려보면 0 < x < 1 부분에서 음수를 가진다.
∴ 참

4)
정수인 어떤 x에 대하여, x^2 < x 이다.
0 < x < 1 범위에서 음수를 가지는데, 정수는 0 < x < 1 범위에 들어가지 않는다.
∴ 거짓

 

Q. (직접 증명)
n이 짝수이면 3n + 5는 홀수임을 증명하라
(힌트: n = 2k로 두고 3n + 5가 2(어떤 정수) + 1 형태로 표현될 수 있는지)

n = 2k 로 두자.
그러면 3n + 5 = 3(2k) + 5 이 된다.
교환법칙으로 2(3k) + 5 가 되고 여기서 임의의 수 p 를 넣어서 2(x) + 1 형태로 만들어보자.
2(3k + p) + 1
-> 2(3k) + 5 가 된다.

여기서
2p + 1 = 5
-> p = 2
따라서, 2(3k + 2) + 1 의 형태로 나타날 수 있게 된다.

괄호 안의 어떤 수가 들어가든 앞의 계수가 2 라면 짝수가 된다.
여기서 + 1 을 더하면 홀수이므로 n이 짝수면 3n + 5는 홀수이다.

 

Q. n이 홀수이면 n^2 + n 은 짝수임을 증명하라.

 

Q. m이 짝수이고 n이 홀수이면 2m + 3n은 홀수임을 증명하라.

 

Q. (대우를 증명)
자연수 n에 대해, n^2 + 5가 홀수이면 n은 짝수임을 증명하라.
(힌트: 명제 대신, n이 홀수이면 n^2 + 5은 짝수임을 증명한다.)

 

Q. n^2이 짝수이면 n은 짝수임을 증명하라.

 

Q. (경우를 나누어 증명)
자연수 n에 대해 n^2 + 5n + 3은 항상 홀수임을 증명하라.
(힌트: n이 짝수인 경우와 홀수인 경우를 따로 증명한다.)

 

Q. n^2이 3의 배수이면 n은 3의 배수임을 즘명하라.

 

Q. n이 홀수이면 n^2을 8로 나눈 나머지는 1임을 증명하라
(힌트: n을 4로 나눈 나머지가 1인 경우와 3인 경우로 나누어 보자.

 

Q. 어떤 자연수를 제곱하여도 그 결과를 3으로 나눈 나머지는 2가 아님을 증명하라.

 

Q. (귀류법)
유리수와 무리수의 합은 무리수임을 증명하라.
(힌트: 어떤 유리수와 어떤 무리수의 합이 유리수가 된다고 가정하고 모순을 이끌어 낼 수 있는가?)

 

Q. 루트 2는 무리수임을 증명하라.
(힌트: 유리수가 된다는 것은 기약분수로 표현이 된다는 것이다.)

 

Q. log_2(5)는 무리수임을 증명하라.

 

Q. (수학적 귀납법)
1 + 2 + 3 + ... + n = n(n+1)/2 임을 증명하라.

 

Q. (수학적 귀납법)

 

Q. (수학적 귀납법)

 

Q. 2 이상의 모든 자연수 n에 대해 n^3 - n 은 6으로 나누어 떨어짐을 증명하라.

 

Q.

 

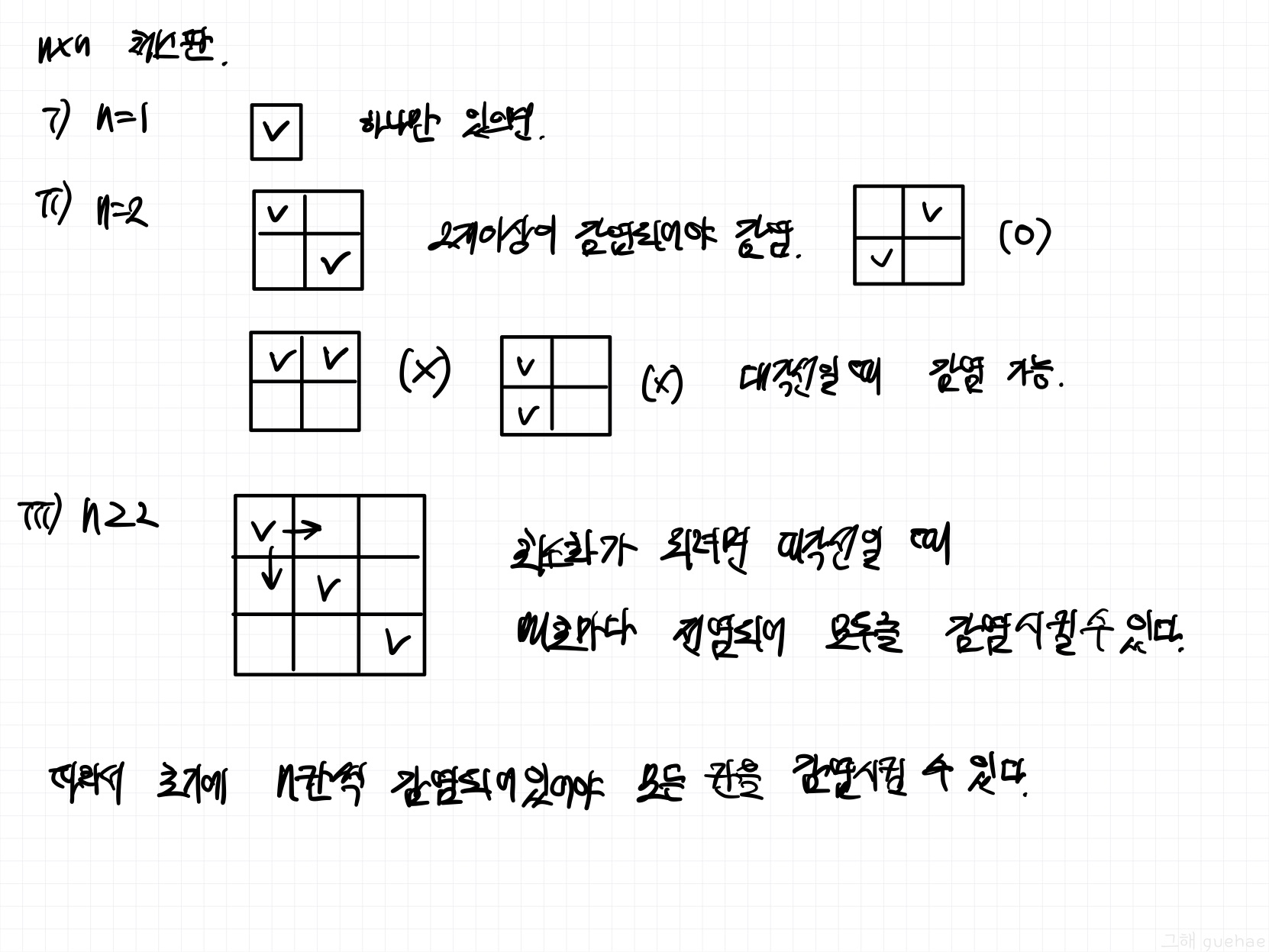
Q. n x n 체스판이 있다. 시작 시점에 일부 칸들이 감염되어 있다. 매초마다 감염이 증가할 수 있다.
규칙은 다음과 같다. 어떤 감염되지 않은 칸은 상하나 좌우로 인접한 네 개의 칸들 중 2 개 이상이 감염된 상태일 때 감염된다. 이 규칙에 따라 모든 칸들을 감염시키기 위해서는 초기에 n개 이상의 칸들이 감염되어 있어야 함을 증명하라.
(힌트: 금방 떠오르는 것은 답이 아닐 가능성이 많다.)

 

 

 

 회고 

드디어 이삿짐 다 옮겼습니다. 옮긴다고 힘들어 죽는줄 알았습니다.

청소도 한번 싹 하고 이제야 한 숨 트이는 기분..

근데 푼 것들 보니까 악필 미쳤네요

제가 항상 노트북으로 필기를 하는 이유입니다.

 

 

 

# SWEA 논리와 증명 # computation thinking # 체스판 # swea 증명 # 싸피 논리와 증명

---